I have been meaning to do this post for several years, but until now I have not found a particularly relevant time to do it. In his recent post at the Air Vent, Jeff Id makes the following statement:
Think about that. We’re re-aligning the anomaly series with each other to remove the steps. If we use raw data (assuming up-sloping data), the steps in this case were positive with respect to trend, sometimes the steps can be negative. If we use anomaly alone (assuming up-sloping data), the steps from added and removed series are always toward a reduction in actual trend. It’s an odd concept, but the key is that they are NOT TRUE trend as the true trend, in this simple case, is of course 0.12C/Decade.
The actual situation is deeper than Jeff thinks. The usual method used by climate scientists for doing monthly anomaly regression is wrong! Before you say, “Whoa! How can a consensus be wrong?”, let me first give an example which I will follow up with the math to show you what the problem is.
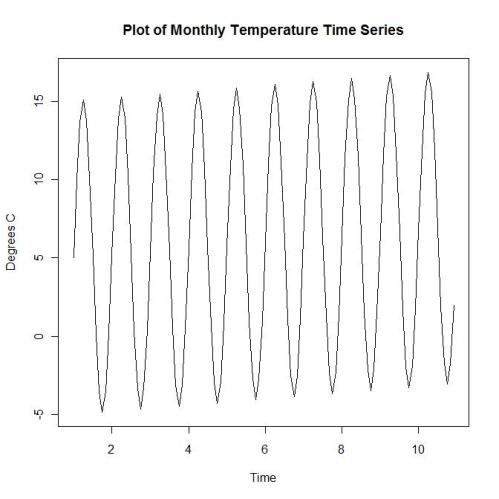
We first produce a series of ten years of ten years worth of noiseless temperature data. To make it look realistic (not really important) we will take a sinusoidal annual curve and superimpose an exact linear trend (of .2 degrees per year) on the data:
We now calculate the anomalies and fit a linear regression line to the anomalies. The following is a plot of anomalies with a regression line:
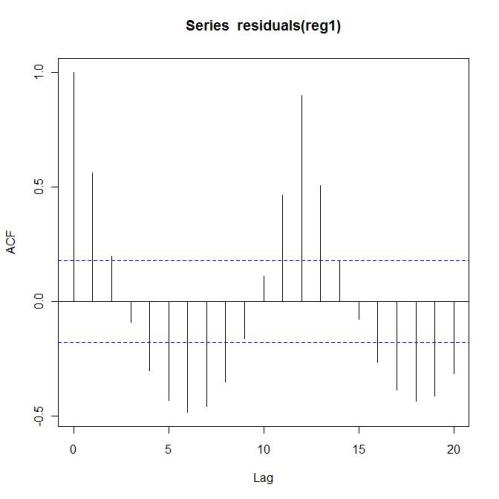
The resulting trend of .198 does not match the actual trend in the data despite the fact that there is no noise present in the series. Although the difference in this case is not large (a poor oft-repeated justification), this is an uncorrectable bias error. What is not as obvious is that this will have an impact on the autocorrelation in the situation as evidenced by the ACF of the residuals – an effect due to the methodology and not inherent to the actual “error” sequence:
But it gets worse. If we change our starting month (but still use ten full years of data), we get different slopes for each month:
| Month | Intercept | Trend |
| 1 | -1.27983 | 0.198014 |
| 2 | -1.28521 | 0.198931 |
| 3 | -1.28971 | 0.199681 |
| 4 | -1.29331 | 0.200264 |
| 5 | -1.29595 | 0.200681 |
| 6 | -1.2976 | 0.200931 |
| 7 | -1.29822 | 0.201014 |
| 8 | -1.29775 | 0.200931 |
| 9 | -1.29618 | 0.200681 |
| 10 | -1.29344 | 0.200264 |
| 11 | -1.2895 | 0.199681 |
| 12 | -1.28431 | 0.198931 |
The average is equal to .2 so all is not lost. However, all of the errors are a result of how we chose to do our analysis and were not really present in the original data.
So what’s causing the problem?
Here comes the math
What most climate scientists still do not seem to understand is the need to spell out the parameters and how they relate to each other. Unless such a “statistical model” exists, we do not have a good grasp of what is happening when we carry out an analysis and a reduced ability to recognize when something is not quite right. The implicit model in this situation is
where
X(t) = temperature at time t
t = y + m, where y = year and m = month (with values 0/12 , 1/12, …,11/12)
µm = mean of month m
β = annual trend
ε(t) = “error” (which in this case are all zeroes).
Now, what happens when we calculate anomalies? If A(t) is the anomaly at time t,
where the “bar” represents averaging over that variable.
Here,
and if we substitute this in the original equation we get
The important thing to realize here is the the month no longer appears with the trend – only the year (and NOT time) should be used to get the correct trend. By using time, we actually are fitting the line
for which the intercept should be different for each month. Since the usual anomaly regression fits a single intercept, the resulting trend is incorrectly estimated.
How can this be fixed?
Several fixes are possible. The simplest is to use year rather than time as the independent variable in the regression. This may seem counterintuitive, but it takes the anomalies and lines then up vertically above each other solving the problem that Jeff noticed. However, this solution can still be problematical if the number of available anomalies differs from year to year.
A better solution is to do the anomalizing and the trend fit at the same time. This corresponds to a single factor Analysis of Covariance where month is treated as a categorical factor with twelve levels and time (or year!) is treated as a numeric covariate. This can be implemented in R using the function lm.
The script used in the post follows:
#we construct 11 years of data for later use
seasonal = 5 + 10*sin(pi*(0:131)/6)
#add trend of .2 degrees per year
trend = (0:131)/60
temps = ts((seasonal+trend)[1:120],start=c(1,1),freq=12)
time.temp= time(temps)
plot(seasonal,type="l")
plot(temps, main="Plot of Monthly Temperature Time Series", ylab="Degrees C", xlab="Time") #anomregfig1.jpg
#function to calculate anomaly
anomaly.calc=function(tsdat,styr=1951,enyr=1980){
tsmeans = rowMeans(matrix(window(tsdat,start=c(styr,1),end=c(enyr,12)),nrow=12))
tsdat-rep(tsmeans,len=length(tsdat))}
anom = anomaly.calc(temps,1,10)
#anomaly regression
reg1 = lm(anom~time.temp) # intercept = -1.180, slope = 0.198
plot(anom, main = "Anomalies",ylab = "Degree C",xlab = "Time") #anomregfig2.jpg
abline(reg = reg1,col="red")
#calculate autocorrelation of residuals
acf(residuals(reg1)) #anomregfig3.jpg
#set up revolving regressions
tempsx = ts(seasonal+trend,start=c(1,1),freq=12)
timex.temp= time(tempsx)
anomx.all = anomaly.calc(tempsx,1,11)
#function to cycle regression starting points and give coefficients
cycle.reg = function(dats) {
coes = matrix(NA,12,2)
coes[1,] = coef(lm(window(dats,start=c(1,1),end=c(10,12))~time(window(dats,start=c(1,1),end=c(10,12)))))
for (i in 1:12) coes[i,] = coef(lm(window(dats,start=c(1,i),end=c(11,i-1))~time(window(dats,start=c(1,i),end=c(11,i-1)))))
coes}
(all.coef = cycle.reg(anomx.all))
# [,1] [,2]
# [1,] -1.279832 0.1980138
# [2,] -1.285205 0.1989305
# [3,] -1.289710 0.1996805
# [4,] -1.293305 0.2002639
# [5,] -1.295949 0.2006806
# [6,] -1.297599 0.2009306
# [7,] -1.298215 0.2010140
# [8,] -1.297754 0.2009306
# [9,] -1.296176 0.2006806
#[10,] -1.293437 0.2002639
#[11,] -1.289497 0.1996805
#[12,] -1.284314 0.1989305
#fit regression using year
year = floor(time.temp)
reg2 = lm(anom~year)
reg2 #[1] -1.1 0.2
#setup anova
month = factor(rep(1:12,11))
time2 = time(anomx.all)
year=floor(time2)
dataf = data.frame(anomx.all,time2,year,month)
#function to test different month starting points
#using time as a covariate
#column 13 is trend
cyclex.reg = function(datfs) {
coes = matrix(NA,12,13)
for (i in 1:12) {dats = datfs[i:(119+i),]
coes[i,] = coef(lm(anomx.all~0+month+time2,data=dats))} #line corrected
coes}
(anov1 = cyclex.reg(dataf))
#function to test different month starting points
#using year as covariate
cyclexx.reg = function(datfs) {
coes = matrix(NA,12,13)
for (i in 1:12) {dats = datfs[i:(119+i),]
coes[i,] = coef(lm(anomx.all~0+month+year,data=dats))} #line corrected
coes}
(anov2 = cyclexx.reg(dataf))


Roman,
So you’re fitting each month separately and then the slope is the mean of the 12?
I am not sure which part of the post you are referring to.
If it is to the (correct) Analysis of Covariance approach at the end of the post, then, no. The fit is to all months simultaneously allowing for a different intercept for each month, but using the same slope.
If to the 12 month table in the middle: This illustrates what happens if I fit the usual anomaly regression starting at a different month each time, but using a full 120 consecutive months. The differences in trend are related to starting at a higher or lower point in the annual temperature.
Roman,
There seems to be an extra line in the code, unless I’m missing something.
for (i in 1:12) {dats = datfs[i:(119+i),]
coes[i,] = coef(lm(anomx.all~0+month+time2))}
dats = doesn’t seem to do anything.
Re: Jeff Id ,
Sorry about that. it occurred when I “simplified” my original script. It should read:
coes[i,] = coef(lm(anomx.all~0+month+time2,data=dats))}
The same correction applies later in
coes[i,] = coef(lm(anomx.all~0+month+year,data=dats))} .
I’ll fix the original script too. To quote the climate change mantra: it doesn’t change the results. 😉
I just spent the last several hours figuring out how the factor class works in a linear regression. I don’t know how you learned so much R but you are awfully good at it.
Re: Jeff Id ,
It really is pretty simple stuff. Using factors in a regression is really just using indicator (0,1) variables. Each category (usually called a level) of the factor has its own indicator. You can adapt this approach to many types of problems (including treering series analysis).
In the two functions at the end of the script there are 12 indicator variables plus the trend. By the way, I did not mention this in the main post, but one does not need to calculate anomalies in advance to estimate trend. The analysis of covariance approach to the actual seasonally unadjusted temperatures will produce the same trend.
I have taught complete courses (usually called Linear models and/or Design of Experiments) on this material so I have a reasonable handle on the mathematics behind it. Transferring this experience to implementation in R is then not as difficult as it may appear. 😉
Thanks Roman,
It’s impressive to me because I get the concept of what you’re doing, including the fact that anomaly is not necessary, and were I to attempt to write this script it would have been difficult for this grumpy engineer to even find where to start in R. Since Climategate SteveM has stopped the technical posts and there hasn’t been that much interesting stuff to learn in blogland, this has been a nice change.
Now I’m curious about how the trends in the various anomaly graphs thrown at us are affected. It won’t be hugely different but it’s like the ‘correct’ trend vs an approximation.
Little lightbulb- I will be thinking about treerings.
My take on this is:
1. As you say, the sinusoid is irrelevant. You’d get the same result with a linear trend
2. What happens is that the trend gets into the monthly anomaly base function. Without seasons, average December is warmer than average January. The monthly mean is a sawtooth function, amplitude 0.2C, period 12 months.
3. This sawtooth function itself has a very small trend, positive or negative depending on which phase it starts in. When subtracted, it makes a corresponding small change in the result.
4. An adequate and simple remedy would be to calculate the monthly anomaly base on detrended data.
5. The effect on an aggregate would be exceedingly small. The sign of the trend difference depends on the starting and finishing month. If these are scattered in a station population, the 1% or so effect that you observe will be much reduced by cancellation.
I couldn’t find code or results for your single factor analysis of covariance?
Re: Nick Stokes (Mar 19 01:19),
OK, I see the code for analysis of covariance is in the cyclex functions.
Re: Nick Stokes ,
I am not clear on exactly what your points are here. Are you saying that it is OK to continue to use a flawed method because in your view the error is “exceedingly small” or “an adequate and simple remedy” can supposedly fix part of the problem?
Anomaly regression as currently used produces bias errors and induces some level of autocorrelation into the results. All of these errors are caused purely by choices made by the analyst and notby inherent problems with the data.
It is not like people are doing these analyses by hand and it is much less calculation to do the simple regression. No extra programming or statistical expertise is required to use the approach I suggest and it has the added advantage of being able to adapt to missing values in the base anomalization period better than simple regression. Furthermore, it can be used directly on the unanomalized data.
What the @#$$ is wrong with just doing it right???
What the @#$$ is wrong with just doing it right???
Grumpy statistician, I like it.
[RomanM: Not as grumpy as it might look. If you check the “spelling” of the expletive, you can see that I used a mild one. 🙂 ]
Re: RomanM (Mar 19 08:35),
“No extra programming”
There’s obviously some. It may be minor in R, but that’s not what they use. In Fortran you could attach an external package, but there would be costs in run time, which may be a problem for a few thousand stations.
Nick, this 2010 not 1980. Surely, you are not serious that this would be some sort of difficult obstacle to overcome.
Maybe, one of their undergrad students could show them how to do it after taking a relatively basic statistic course taught by a statistics department.
From my personal experience of over 40 years working in an academic environment, the real problem is the insular nature of statistics in climate science (although they are certainly not alone in that). There is a tendency to teach their own stat courses regurgitating methods that were originated at a time when what you refer to may have been true. Methods were invented without a full understanding of their implication and these proliferated and became the standard for the subject. Very few statistician names ever appear as coauthors on their papers so fresh blood rarely enters the system.
In their defense, you can’t just go out, pick a statistically knowledgeable person up off the street and expect instant results. However, IMO, it is a lot easier for a statistician to learn enough climate science than for a climate scientist to educate themselves sufficiently in statistics in moving the subject forward.
Roman this rings true with my experience.
The issue comes most clear when you see that for the most part a statistical model is never formulated. Statistics is viewed as a “cook book”
Let’s grant that the effect would be exceeding small. Let’s also grant ( as Nick seems to do ) that
Roman’s math is correct. The method is described in math and code is provided. Now, what engineer in the crowd would NOT use a better method?
What engineer in the crowd doesnt’t care about that last 1%?
It’s this attitude, ( doing it right doesnt matter ) that causes a lack of trust in certain circles. People who have worked on that last 1% know that people who are sloppy about that are more likely to sloppy about bigger errors. That’s why you check their work. That’s why you audit their work. thats why you want their code.
Since 2004 or so the wars between AGW types and “skeptical” types has been dominated by issues like this. In all cases the AGW types have had two choices: Given choice 1, they opted for 2
1. Thanks for the improvement.
2. Your improvement will not be accepted
because some other person said your improvement disproved AGW and that puts
you in league with people who deny AGW and therefore you must have gotten oil money. In anycase, we won’t say your name, Roman, so there! And while you’re at it Roman can you disavow all people who have ever linked to your
work? And why dont you go criticize spensers work? and blah blah blah.
Early on Mann laid out a strategy ( Overpeck as well ) do not legitimize anything done by a skeptic or somebody related to a skeptic. regardless of the truth. The truth is subordinated to the maintenance of tribal identification. This strategy was passed on at the highest levels of the tribe. Lower beta chimps play monkey see, monkey do. They don’t have to get the memo.
Time will pass, maybe some grad student will independently discover this method. Then it will be accepted, but only if he publishes with an alpha chimp.
[RomanM: I only saw your comment after I posted my response. Contrary minds think alike, except I thought that it could be done by a good undergrad. 🙂 ]
Re: steven mosher (Mar 19 15:35),
Steven, I agree that Roman has described a very simplified problem and provided code to solve it. As far as math goes, he has just referenced an analysis of covariance approach, and some more substantiation that it does solve some real problem in all circumstances would be useful.
‘
What is lacking is code that could be used in some actual circumstances that can be pointed to in climate modelling practice. I’ve queried below whether anyone actually does what is described here – forming a single-station anomaly series and computing a trend by regression on the series of monthly values*. Some may have done this, but I’m unaware of it as a major activity. I certainly don’t see how either the problem or its solution relates to what is done in the major indices.
Though I do think that it might be better to calculate the anomaly bases using detrended data. One would need to check whether there was a real benefit to offset the extra computing time.
* In fact I’d go further – I don’t see why anyone would want to do this. The main point of anomalies is to facilitate combination of stations. If you want the trend of an individual station, simple temperatures are better.
Pingback: Roman on Anomaly Trend Regression « the Air Vent
Maybe one objection to doing it right rather than just making a first order correction is that it is simpler to understand for the non-statistician? Not a valid reason, but maybe a worthwhile cross-check for someone who can’t code up the correct regression. I’m wondering what the impact is when the underlying trend is not linear (and of an unknown form)…
I don’t buy that objection. There are several simple ways it can be explained to someone with little statistical experience.
If one can understand a regression as fitting a line to a set of points, then one could visualize fitting 12 lines to the data (one for each month) with a common slope and 12 possibly different intercepts. As far as coding up the correct regression, people had to learn how to programme up the simple regression at some stage. The one I propose is no more complex.
For instance, in R, lm(temperature~month+time) doesn’t look any more complex than lm(temperature~time) to me. Most of the statistical programs in use have such simple versions of these as well. Besides, you wouldn’t even have to learn how to calculate an anomaly. 😉
There are many reasons not to do it the traditional way. Although it wasn’t possible to show this using “noiseless” data, when you use real data, choosing different periods for anomalization will generally produce differing trend estimates – not a good thing in my book.
As far as using linear fits when the underlying trend is of a different form, the anacova version won’t be any worse than the usual anomaly regression. It might be interesting to cobble up a version of lowess fitting including factors to create a more general approach. Hmmm…
As a non-statistician I have to disagree. If the results are in error, then the non-statistician meanders off with a mistaken notion of what is going on with the data and the system it was collected from thanks to the laziness of the analyst. Worse is that whoever conducted the original (erroneous) analysis usually assumes they did it right to begin with. This one reason that the process of “peer review” has to be taken seriously. Statisticians should have been included in the peers for many of the published AGW papers. They weren’t, quite likely because the authors did not want to hear what they did wrong, and were well aware that compared to a real statistician they were mere amateurs. Thus the AGW “peer review” process was really a post-modern, politically correct, process of validation rather than true scientific review. The CRU emails actually appear to document this behaviour very well.
RomanM, there is nothing wrong with doing it right of course, everything else being equal.
Sometimes “right” is either impossible or impracticable, in which case you are left developing a method and associated sensitivity analysis that (hopefully) shows that the “warts” with the method don’t substantially inflate either the bias or the error of your parameter estimations.
But there is no great defense to having two algorithms, one which does it correctly and runs in roughly the same amount of time as the original code.
This is interesting and something I never have been aware of. I have been playing around with this in Matlab and I think another way of fixing the problem is to use annual means (without ever calculating the monthly anomalies) and then regress these with years*. Or maybe this is just equal to what you suggest as the first solution?
Using running means over 12 values also gives the correct trend.
I am not defending to do it one way or another – just trying do deepen my understanding.
*) From these yearly means one can of course also calculate anomalies compared to the mean of the yearly means.
It is certainly OK if one wishes to look only at overall annual trends. However you lose the information on the seasonal behaviour of those trends – e.g., does the increase or decrease behave differently over the summer as opposed to the winter. When no values are missing and there are equal numbers of observations in each month, the average of all 12 monthly trends will be exactly equal to the annual trend due to the mathematics involved. However when the data is incomplete, this will not be the case (nor will you be able to simply calculate proper annual values for each year). The method that I am proposing can still handle those situations.
Although I have not previously looked at fitting a trend to the moving averages, it is immediately obvious that several problems will arise. Again, missing values will cause difficulties. There will be end effects due to the fact that observations in the middle of the series will affect 12 of the moving averages, but the 11 points at either end will participate in fewer – the two end values are only used once each. Finally, if you do a regression on the moving average series, the estimates of the variability of the trend (used for testing and confidence intervals) will be incorrect due to the fact that the series is highly correlated and the estimates of the usual regression assume “independent” values. This would require a somewhat complicated adjustment.
I am aware that calculating a moving average introduces problems with end effects and autocorrelation, and this should be considered when calculating confidence intervals.
I just noticed that the 12-month moving average gave me the correct trend using the same test example as you.
What if you calculate the anomalies with respect to the whole series, e.g.
anomaly(i)=data(i)-mean(of all data points)
It is all that “consideration” of end effects and auto-correlation that makes the use of procedures involving moving averages less desirable. Simpler is usally better.
The reason for this is that there is no”noise”, ie. randomness in the example data. Otherwise, that would likely not be true.
Calculating anomalies with respect to the entire length of the series is generally a better idea than using a shorter period because it lowers the variability of the anomaly series and lessens the effect of possible aberrant temperature variations during the base period. However, the problems with getting incorrect values for the trend would still remain.
The trillion dollar question.
Have you tried this with GISS data etc?
I have looked at several, to see what happens, however, my focus has been mainly on the theoretical end of the methodology.
GISS is left as an exercise for the reader. 😉
Don’t leave it for this reader !!!!!!!
My pea sized brain would explode.
I was just just curious as to what the difference would be between doing it right and fudging it !!!
Mpkr.
You should not expect any significant difference between Roman’s method and the other methods used. By significant I mean this:
The temperature record will still show warming.
That warming will still be significant. What the improved method gives is a way to treat certain pesky problems differently and more accurately.
There are these types of issues with Global temps:
1. Accurate methods for calculating the average and all the associated errors.
2. Accurate accounting for the errors introduced by adjustments and corrections of raw data.
3. Accurate metadata.
Roman is focused exclusively on number 1.
His work will will help on #2.
Re: RomanM (Mar 19 13:40),
At http://oneillp.wordpress.com/2010/05/04/romans-anomaly-regression-and-gistemp/ I have started a series of posts attempting this exercise, and at the same time providing a detailed example of the GISTEMP anomaly and urban station adjustment procedures which may be useful for anyone who would like to learn more about these procedures, but does not have the time or inclination to wade through the FORTRAN code.
There’s a lot of talk in the press about how AGW wasn’t sold to the American public properly. I think this is hogwash. The American people woke up when they discovered that they were going to have to pay dearly to “prevent” AGW.
America smelled a rat when they heard that they had to pay to prevent this catastrophe that would occur in 100 years from today.
The only reason, in my mind, that AGW got as far as it did, was because of the “sausage making” involved in the data manipulation.
The cornerstone of the data manipulation is calculations of anomalies! Seriously, even with my statistics & engineering background, my eyes glaze over with all the massaging, averaging, substitutions… etc, etc.
If you want to be an Anomaly Wonk, keep going. If you want to convince the public that the earth isn’t warming due to mankind’s use of his vast inventions, use a pure number. The Number will stick in peoples heads & they will reject the real sausage making of the Warmers.
Respectfully submitted!
“However, IMO, it is a lot easier for a statistician to learn enough climate science than for a climate scientist to educate themselves sufficiently in statistics in moving the subject forward.” This is a telling comment. As a non-scientist and even more of a non-statistician, it has become clear to me that “climate science” (as distinct from climatology, paleontology and the various other “ologies” that comprise it) has been misrepresented, both to the public and to itself.
The public, by and large, thinks of “climate science” rather vaguely as “climatology on steroids”.
The soi-disant climate scientist thinks of climate science as a lot of climatology, paleontology, etc, (whatever discipline he has come from) enriched by a bit of statistical analysis. The real “science” he feels, lies in its practitioners’ disciplines-of-origin. Most of it may indeed be uncontroversial, endowing the “science-is-settled” mantra with a plausible veneer, and populating the field with workers who were at best mediocrities in the very skill – statistics – in which they needed to excel.
The truth seems to be that climate science is really a bit of climatology, paleontology, etc., (mostly uncontroversial) enriched by a lot off statistics (very controversial), and should accordingly be practised by people with the best statistical skills available.
Reading, if not comprehending, the comments on this page, I can well undersand how unwelcome the Tree Ring Circus must have found the irruption of competent statisticians into their (statistically) cloistered world.
The usual method used by climate scientists for doing monthly anomaly regression is wrong! Before you say, “Whoa! How can a consensus be wrong?”
Roman, I’ve been wondering what activity of climate scientists you are talking about. Do you have examples? I’m wondering who exactly should mend their ways and what they should actually do to reform? Where is the “consensus” expressed?
Your example relates to taking a set of station values, computing an anomaly presumably by CAM, and then running a regression through the serial monthly anomalies for individual stations. But who does this? Not Gistemp – I don’t believe they compute trends anywhere, and they use a more complicated anomaly procedure. They do not output station anomalies. It’s true that someone who used their output monthly regional anomalies in this way might encounter some version your problem (I’m not sure). But it isn’t clear how your remedy could be applied. It would, however, be fairly easy to detrend the data in the initial anomaly calculation of toANNOM.f.
People seem to do this type of calculation on a regular basis. Whether GISS uses it, I don’t know. However, I do know that the temperature keepers have in some cases provided linear trends for grid cells – I have seen maps representing such gridded trend values. How would you think these might be calculated? Might the same problem not be inherent here?
As an aside, you seem to constantly focus on your role as public defender of the AGW movement. Does not your scientific side ever become involved in the mechanics of the methodology used? Did you not find it at all interesting (and initially quite counterintuitive) that anomalizing series induces these effects in a regression? For me, that fascination of discovery and understanding is exciting and typifies what real science is all about. Maybe this is one of the differences between “believers” and “skeptics”. 😉
By the way, just how would you “detrend the data” before anomalizing or am I misunderstanding your final sentence.?
Re: RomanM (Mar 20 15:36),
Did you not find it at all interesting (and initially quite counterintuitive) that anomalizing series induces these effects in a regression?
Yes, I did. I too was surprised by your staircase plot. That’s why I figured out what was causing it, and wrote my interpretation. I also figured out the direct remedy, which is detrending the data prior to calculating the anomaly base (your m(t)).
By detrending, I mean the usual process of fitting a linear trend to the temps in the base period, and subtracting a zero-mean version to calculate m(t). This directly fixes the problem you have described, and is easily implemented in any programming environment.
I do defend climate scientists when they are accused of some incorrect process without proper attribution. You spoke of a “consensus” way that was wrong, but don’t seem to have any examples at all of them actually doing it.
It seems neither you nor I know whether grid cells would have the same issue. I do know that if they do, it would be very small indeed. Your 1% already overstates the issue, because you have used a 10 year base. Climatologists use at least thirty years, which brings the range of variation down to 0.33%. Then when you average the effect over a sample with varying starting times (which varies the sign), that makes it a lot smaller.
Re: RomanM (Mar 20 15:36),
m(t) – I was thinking of another post – here it’s the estimate of μm.
Keep at it RM
Tx from the rest of us geeks
Tim
Nick Stokes,
The flaw with this is that the “detrending” regression is subject to a similar problem that causes the anomaly regression to produce different trends which vary according to which time of year the data starts and ends. Because the data still contains seasonal variation, if you start at a cooler time of the year, the trend will be higher and a start at a warmer time underestimates the trend. This effect can be pronounced since you are dealing with raw data that may have variation an order of magnitude larger than the corresponding anomalies.
The overwhelming message in the series of posts on combining series and/or doing anomaly regression should be that it is better to use a procedure which simultaneously estimates both the “adjustments” and the end result of whatever the procedure is attempting to do. This avoids the multitude of problems that stem from the sequential nature of many of the current procedures. Initial “errors” in the process will not proliferate through the sequence of operations in a “black box” fashion and error bounds become more easily and accurately calculable.
The current methodology comes from a time when computer capability was substantially lower and designed mainly by people for whom statistical techniques were a “second language”. The amazing growth in the power of computing in the last twenty years has revolutionized the area of statistics. Many procedures we take for granted now were theoretically possible, but not practical to implement. Statistics has improved due to the adaptation to these new capabilities, but, IMHO, this does not appear to be the case with processing the data from the temperature record.
I am not predicting huge changes in the results, but it would be nice to move the science forward to see what happens when solidly based procedures replace some of the ad hoc adjustments of the homogenization variety.
Pingback: Demonstration of Improved Anomaly Calculation « the Air Vent
Nick,
Your answer about detrending the data is also imperfect. Detrending the seasonal data before calculation of anomaly would probably improve the situation in most cases, but would not correct it. The only way to correct the step problem would be to detrend with the ‘correct’ trend in the first place, which means using a method as shown above.
Re: Jeff Id (Mar 22 08:08),
Jeff, it doesn’t have to be perfect. According to your demonstration example, the difference in trend estimate between starting from starting from detrending with zero trend (ie raw) vs “getting it right” is about 2 parts in 1000. If you start with a detrend that is only 99.8% correct, the error then would be about 4 parts in 1,000,000. OK, that’s imperfect, but you could iterate…
None of it has to be perfect. It’s pretty easy to call the regression defined by Roman in R though. I’m sure Matlab isn’t any more difficult.
My example could probably have demonstrated a much greater difference, I simply took the first curve I tried. It felt like ‘hiding the decline’ in reverse to look for a stronger example and I was lazy after working on this stuff (not the post itself) for so long.
It’s only those who understand the math who would be likely to use the improvements anyway so a perfect example didn’t seem required. Maybe I was wrong though.
Re: Nick Stokes ,
I don’t understand how you can pursue this line with a straight face. What is so difficult in saying, “Yah, it is always a good idea to estimate all of your parameters simultaneously”.
It’s not like what I have been suggesting is oh-so-computationally-intensive-and-beyond the abilities-of-all-but-a-few. Did it ever occur to you that improvements are possible? I don’t object to people finding fault and correcting what I do, but to side-step it in what appears to be some fatuous attempt at protecting the “established procedures” strikes me as ridiculous.
Surely, there must be times when your scientific side actually comes out and suppresses the propagandistic side.
“…with a straight face”
Well, my face wasn’t quite straight, hence the dots. I’d have used a smiley, except that blogs make them too big and distracting. My amusement was at the prospect that there might be an argument about an error of 0.0004% in this context.
But I’m glad you put “established procedures” in quotes. You haven’t been able to show a case of any scientist doing it, and I don’t believe they do. It doesn’t make sense to form an anomaly on station data in order to calculate the trend. The raw data is simpler and better for the purpose. So I don’t believe I am defending the status quo. I’m not really defending, and it isn’t the status quo.
Why I have been interested is because it might affect the proper use of anomalies, which is in combining data from different stations. Because the data availability doesn’t match, either at the ends or with missing data within the station periods, you need to make sure that the arithmetic you do in merging would be the same if you replaced missing data with your best estimated value. Since working with missing data naively generally effectively assumes it is zero, it is desirable that for an anomaly series the best estimate of any missing value is indeed zero, and I was wondering if this small ripple that you have noted might affect that.
I think the answer is, mostly no. The important issue which probably could be treated better is not whether the static monthly anomaly that is subtracted has a trend over the 12 months, but rather whether the best estimate of missing data should make an allowance for trend as well a monthly mean. That involves different arithmetic.
hey Roman you will like this
Unit roots in temperature series
Pingback: GHCN Global Temperatures – Compiled Using Offset Anomalies « the Air Vent
Roman,
Mistakes in climate science are of no interest
even when they matter.
http://bishophill.squarespace.com/blog/2010/3/26/false-alarm.html
See keenan’s update
One should be calculating the z-score, i.e., subtracting the mean from the series and dividing by standard deviation. But there appears to no mention of the magnitude of the error – and it certainly isn’t constant – and it’s certainly not equal to zero. Since there’s nothing anomalous about natural variation, the fact that climatologists refer to the z-score as an anomaly speaks to their bias. The most disappointing aspect of this blog is the use of the work “Statistics” in its title. I was hoping to get away from junk science and actually see the error bars propagated from the uncertainty in the original data.
Re: Agile Aspect ,
The error bars can be calculated directly from the procedure, although I have not provided them at this point.
I am not sure what exactly you are referring to about “calculating the z-score” with regard to an anomaly regression. If you are referring to the difference in variability over the various months, this can be taken into account, but not by “standardizing” the data with z-scores prior to applying the procedure. Rather, a weighted regression is used with the weights depending of the variability.
An “anomaly” (bad choice of word, I agree) is typically a difference from a center and no scaling is involved. Scaling before doing the regression is very poor procedure.
… back to the Dominican golf…
I am new here. I have few questions particularly about your comments “Rather, a weighted regression is used with the weights depending of the variability.” for difference in variability over the various months. Lets assume that I have 10 stations for my land called X. I have annual (lets forget here about the monthly values) T data from 1960-2012. I have two cases here, some of stations have missing years. For this case, i have calculated anomaly (from yearly T average: Ti-T(average of 1960-2012)) of each station then average across the 10 stations to calculate long term trend and inter annual T variation for country X. The yearly anomaly averaging is from only those stations which have record for that specific year (meaning the number of stations vary each years). Case two, using only few stations which have the full 1960-2012 records. Here I do the same, calculate site level anomaly, then take average across the stations for each year. from this I can calculate the regression slope (trend), and inter-annual T difference. The problem here is, some stations have very large anomaly, so when I do linear averaging of anomaly across the stations do I have to weight with magnitude of each site-year anomaly (is that what you are suggesting above). I can not average T across sites before analysing anomaly, because each instrument has bias, and should be contained by first doing site level anomalies. Question two, due you have any suggestion for averaging the anomaly when I include sites with few missing records? i am positing this questions for all the participants here.
When calculating monthly temperature anomalies, you first calculate the averages over a specific set of years for each of the twelve months. These average values are then subtracted from each of the terms of the entire series. What some people may not realize is that the variability of the original monthly values (and therefor the anomalies as well) may vary from month to month depending on the latitude and other geography of the location where the temperature is measured. For example, the variance of the monthly average temperatures at a station in the Antarctic can be almost four times as large in June or July (the middle of their winter) as that for the month of January. Near the equator, however, the variability of temperatures from month to month tends to be somewhat more constant.
The “weighting” that I was referring to applies to the application of the regression procedure when applied to a single sequence of temperatures (either anomalies or to the raw series as described in the post). To account for the differences in monthly variation, we can estimate trends using a weighted regression using a weight for each month that is proportional to the inverse of the variance of the series of monthly averages for that month. It is not related to the situation of averaging several series together as you refer to. Weighted averaging of series would be used if one were to calculate area weighted averages however the weights in such a case would be determined by the areas represented by each sequence and not by the properties of the series themselves.
As far as averaging series with missing values, I don’t find any of the methods involving anomalies particularly appealing. I use my own method which allows for missing values, does not require a common overlap period for all of the series and results in an average temperature series for which anomalies can be calculated should they be desired.
Pingback: Roman’s Anomaly Regression and GISTEMP « Peter O'Neill's Blog
First time on your blog. Interesting approaches, by a seemingly well-qualified critic. Would you care to post your real name, and a link to your CV & publication list?
I share your concern with the repeated misuse and misunderstanding of basic statistical techniques in climate science. I did a statistical analysis of geochemical data for my M.S. (mumble) years ago. Sadly my knowledge of geostatistics is now very rusty. But I can recognize ignorance, sloppiness and arrogance — Michael (Mannomatic) Mann and Phil (where’s my data?) Jones are the poster children here, sigh.
Keep up the good work. Science is (eventually) self-correcting, but it can take a maddeningly long time.
Kind regards,
Peter D. Tillman
Consulting Geologist, Arizona and New Mexico (USA)
Although I do not overtly hide my identity – it has been posted several times on CA – I am leery of crazies such as the one who recently bothered Anthony of WUWT. Some information about me can be found on Jeff Id’s the Air Vent. I will drop you an email.
The good news is that the “ignorance, sloppiness and arrogance” are all too easy to recognize. The bad news is that it is much too common.
Pete,
Roman is a careful statistician. He’s done some very interesting work here from my less educated perspective. I’ve been holding my breath for my coauthors to get a publication through what seems to have become a gauntlet on the Steig antarctic reconstruction but hope to apply Roman’s methods to surface stations for an antarctic trend.
Pingback: Global Warming Contrarians Part 1.1: Amateur Temperature Records « Planet James
Old post but it was cited. I think I saw this when it was new but said nothing. The matter of the elephant, accidental or not?
You state “We first produce a series of ten years of ten years worth of noiseless temperature data.”. Not according to the plot.
’tis one month short, falling foul of the non-integer wave problem and whilst this does not affect the thrust of what you are saying, it might affect compares.
I assume that you are basing this on the fact that in the first plot in the head post, the height of the first point in the plot does not match the height of the last point. However, if you look at the R program you will see the line:
temps = ts((seasonal+trend)[1:120],start=c(1,1),freq=12)
The temperature series consists of 120 points which in my book translates into exactly ten years of measurements.
The reason you may be confused is that the points represent the average temperature for each month. The first month, January, would not be at the same level as the last point in December. There are ten complete cycles.
Thanks Roman, yes I wondered whether that was just the plot. R is inaccessible, so I ignore it.
I’ll wait for a more apt moment to raise what could be a long subject.
Pingback: Estimating yearly trends with an EM algorithm in R | Spatio-temporal modelling
Pingback: Proxy Hammer « the Air Vent
It is now August 2014. I’ve never visited this blog before – which is a pity because I like it. I am continually looking at monthly climate data. I sometimes run “dummy variable” regressions for different intercepts or different slopes (shades of my industrial background in the 1970s and 80s) but I believe that the outcomes are a bit too complex for the typical climatologist to get to grips with ;-). I do all the calculations in my homemade stats package – which, before you ask, gets the right answers (that is, if SAS gets the right answers!). However, is it all not a bit over the top? My approach to a new climate data set is to do some plotting. This elementary ploy often reveals that fitting a linear model to any longish series is akin to nonsense at the practical level. Trends are presumably calculated as guides to future behaviour of the series – that is as a forecasting method. Why else bother with them? When I fit a trend line or lines I invariably compute confidence intervals for the estimated parameters, and produce the corresponding plot, which reveals those observations that fall outside the chosen confidence level. It also frequently shows the futility (or lack of value) of the trend as a predictor of future observations. Many climate observations, especially temperatures either measured directly or arrived at from proxy data (often of very dubious value as substitute temperature observations) seem to have a characteristic that is seldom discussed. It is that evidence for abrupt changes is plentiful. I could provide plenty of examples. Unforecastable onset of a sudden change renders any linear fit effectively useless as a climate indicator, and this is what worries me.
OK – I’ve written too much and will stop. I just hope that someone like Roman reads it!
Robin (Bromsgrove, UK)
Pingback: Temperature Trend Profiles & the Seasonal Cycle | Cha-am Jamal, Thailand
Pingback: Temperature Trend Profiles & the Seasonal Cycle | Thongchai Thailand